Sample-Section 1-Part A-Q1
$
\displaystyle \lim_{x \rightarrow \pi} \frac{\cos x + \sin (2x) + 1}{x^2 - \pi^2}
$ is
分析Analysis
$\displaystyle \lim_{x \rightarrow \pi} \cos x = \cos \pi = -1$, $\displaystyle \lim_{x \rightarrow \pi} \sin (2x) = \sin 2\pi = 0$
$
\displaystyle \Rightarrow \lim_{x \rightarrow \pi} (\cos x + \sin (2x) + 1) = -1 + 0 + 1 = 0
$$\displaystyle \lim_{x \rightarrow \pi} (x^2 - \pi^2) = \pi^2 - \pi^2 = 0$
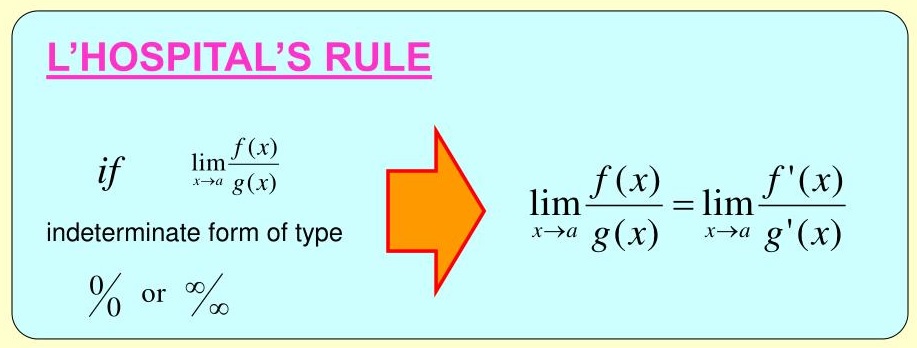
We have form $\frac{0}{0}$, so we can use the L’Hospital’s Rule to solve the problem.
\begin{align}
&\lim_{x \rightarrow \pi} \frac{\cos x + \sin (2x) + 1}{x^2 - \pi^2} \\
= & \lim_{x \rightarrow \pi} \frac{(\cos x + \sin (2x) + 1)’}{(x^2 - \pi^2)’} \\
= & \lim_{x \rightarrow \pi} \frac{-\sin x + 2\cos 2x}{2x} \\
= & \frac{-\sin \pi + 2 \cos 2\pi}{2\pi} = \frac{2}{2\pi} = \frac{1}{\pi}
\end{align}
领取免费学习资料
联系我们CONTACT US


